Physics – Sample Short Answer Quiz
Physics – Sample Short Answer Quiz
Quiz Summary
0 of 10 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 10 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 10
1. Question
1 point(s)(a) The moon Phobos circles Mars in 7 hours and 39 minutes at a distance of 9.5 x 106 m as measured from their centres. Calculate its orbital speed in ms-1. (2)
(b) Explain the issues associated with satellites in low Earth orbits. (3)
(c) Calculate the orbital radius of a satellite in a geostationary orbit, as measured from the centre of the Earth. (2)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 2 of 10
2. Question
1 point(s)Galileo discovered the moons of Jupiter. He could measure their orbital sizes by using the diameter of Jupiter as a unit of measure. He found Io, which had a period of 1.8 days, was 4.2 units from the centre of Jupiter. Callisto, Jupiter’s fourth moon, had a period of 16.7 days.
Using the same units that Galileo used, predict Callisto’s distance from the centre of Jupiter. (2)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 3 of 10
3. Question
1 point(s)It was proposed to investigate the surface of the planet Mars by putting a spacecraft (the command module) into orbit around the planet and sending an exploration module down to the surface of the planet and subsequently recovering it.
mass of planet Mars = 6.42 x 1023 kg
radius of planet Mars = 3.39 x 106 m
(a) The command module is positioned in circular orbit at a height of 5.0 x 105 m above the surface of the planet.
Show that the period of the orbit is just over 2 hours. (2)
(b) Calculate the magnitude of gravitational field strength at a point on the orbit of the command module. (1)
(c) Sketch a graph showing how the gravitational field strength, gM, due to the planet Mars varies with distance from the planet along a line through the centre of the planet. Consider points external to the planet only. (1)
(d) Calculate the change in gravitational potential energy in moving the exploration module of mass 1.0 x 1023 kg from the surface of Mars to a point on the orbit of the command module. (2)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 4 of 10
4. Question
1 point(s)The picture below shows the opening screen of an online activity aimed at teaching Year 8 students the difference between mass and weight.

(a) Assess the statement “Nothing on the International Space Station (ISS) has any weight”. (3)
(b) Calculate the acceleration of a 5.00 x 102kg space probe when it is 4.00 x 105km away from the centre of a planet that has a mass of 2.50 x 1024kg. (3)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 5 of 10
5. Question
1 point(s)A 4.00 x 102 kg satellite completes one orbit around Earth in 2 hours exactly.
(a) Calculate the radius of this satellite’s orbit. (2)
(b) Calculate the gravitational force acting on the satellite. (2)
(c) Explain the nature of the force (i.e., its important characteristics) in relation to the motion of the satellite. (2)
(d) Explain one important advantage of using multi-stage rockets to launch vehicles into space and beyond. (1)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 6 of 10
6. Question
1 point(s)There are several reasons why the value of gravitational acceleration varies at different places on the Earth’s surface.
Describe how the orbit of geostationary satellites would need to change if the Earth rotated faster. (2)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 7 of 10
7. Question
1 point(s)The Mars Reconnaissance Orbiter (MRO) is a NASA probe currently orbiting Mars at an altitude of 300 km above the surface. Among other things, the MRO is used to transmit data from the rovers on the surface back to Earth.
The following table contains data about Mars and the MRO.
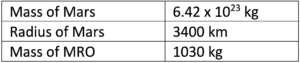
(a) By using Kelper’s Law of Periods, calculate the period of the MRO’s orbit around Mars. (2)
(b) Calculate the centripetal force on the MRO due to Mars, and state its direction. (3)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 8 of 10
8. Question
1 point(s)When it operated, the Space Shuttle was able to attain a low-Earth orbit at an
altitude of several hundred kilometres. However, it was not considered as “escaped” from Earth’s gravitational field.Describe the conditions necessary for a spacecraft to escape Earth’s gravitational field in terms of the energy required using appropriate equations and symbols. (3)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 9 of 10
9. Question
1 point(s)A satellite having a mass of m kg is revolving in uniform circular motion around a certain planet that has a mass M kg. The radius of orbit of the satellite is R metres.
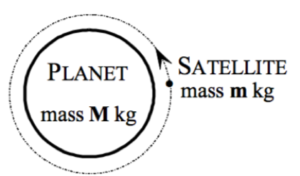
(a) Identify the force that provides the centripetal force keeping the satellite in orbit. (1)
(b) Equate these forces to show that the orbital velocity of the satellite is: (2)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
-
Question 10 of 10
10. Question
1 point(s)Determine the orbital speed of the International Space Station orbiting at 350 km above the surface of the Earth. The radius of the Earth is 6.37 x 106 m. (3)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
-
