Mathematics Standard 2 – Sample Short Answer Quiz
Solutions can be found by pressing ‘hint’
Mathematics Standard 2 – Sample Short Answer Quiz
Quiz Summary
0 of 5 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 5 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 5
1. Question
1 point(s)The graph of the line y = 4 − x is shown.
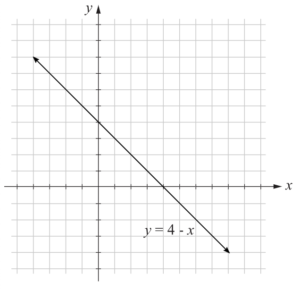
By graphing y = 2x + 1 on the grid provided, find the point of intersection of y = 4 − x and y = 2x + 1. (3 marks)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Hint
Graphing y=2x+1:
y-intercept = 1
Gradient = 2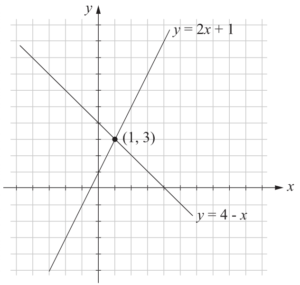
∴ Point of intersection is (1, 3).
-
-
Question 2 of 5
2. Question
1 point(s)Two friends, Sequoia and Raven, sold organic chapsticks at the the local market.
Sequoia sold her chapsticks for $4 and Raven sold hers for $3 each. In the first hour, their total combined sales were $20.
If Sequoia sold x chapsticks and Raven sold y chapsticks, then the following equation can be formed:
4 x + 3y = 20
In the first hour, the friends sold a total of 6 chapsticks between them.
Find the number of chapsticks each of the friends sold during this time by forming a second equation and solving the simultaneous equations graphically. (5 marks)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Hint
Graphing 4x+3y=20
y=−43x+203y-intercept=(0,203)
x-intercept=(5,0)
Gradient =−43Second equation:
x+y=6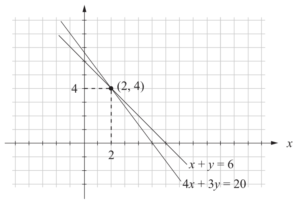
From the graph,
Sequoia sold 2 and Raven sold 4. -
-
Question 3 of 5
3. Question
1 point(s)Temperature can be measured in degrees Celsius (C) or degrees Fahrenheit (F).
The two temperature scales are related by the equation F = 9C/5 + 32.
(i) Calculate the temperature in degrees Fahrenheit when it is −20 degrees Celsius. (1 mark)
(ii) The following two graphs are drawn on the axes below:
F = 9C/5 + 32 and F = C
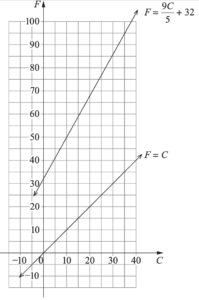
Explain what happens at the point where the two graphs intersect. (1 mark)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Hint
(i) F = 9(−20)/5 + 32
= −4∘F(ii) The two graphs intersect at a temperature where
Celcius and Farenheit are the same. -
-
Question 4 of 5
4. Question
1 point(s)Penny is a baker and makes meat pies every day.
The cost of making p pies, $C, can be calculated using the equation
C = 675 + 3.5p
Penny sells the pies for $5.75 each, and her income is calculated using the equation
I = 5.75p
(i) On the graph, draw the graphs of C and I. (2 marks)
(ii) On the graph, label the breakeven point and the loss zone. (2 marks)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Hint
(i)
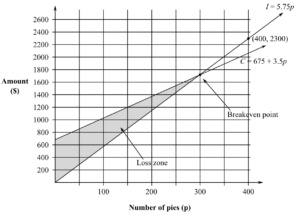
(ii) Loss zone occurs when C>I, which is shaded
in the diagram above. -
-
Question 5 of 5
5. Question
1 point(s)Ashley makes picture frames as part of her business. To calculate the cost, C, in dollars, of making x frames, she uses the equation
C = 40 + 10x
She sells the frames for $20 each and determines her income, I, in dollars, using the equation
I = 20x
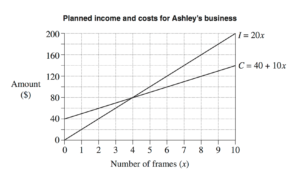
Use the graph to solve the two equations simultaneously for x and explain the significance of this solution for Ashley’s business. (2 marks)
-
This response will be awarded full points automatically, but it can be reviewed and adjusted after submission.
Hint
From the graph, intersection occurs at x=4♦ Mean mark 36%.
MARKER’S COMMENT: The intersection on the graph is the same point at which the two simultaneous equations are solved for the given value of x.
⇒ Break-even point occurs at x=4
i.e. when 4 frames sold
Income =20×4=$80 is equal to
Costs =40+(10×4)=$80If <4 frames sold⇒ LOSS for business If >4 frames sold⇒ PROFIT
-
